블로그를 이전하였습니다. 2023년 11월부터 https://bluemiv.github.io/에서 블로그를 운영하려고 합니다. 앞으로 해당 블로그의 댓글은 읽지 못할 수 도 있으니 양해바랍니다.
반응형
DFS 와 BFS 에 대한 글은 아래 글을 참고한다.
2020/03/29 - [Algorithm] - 그래프 BFS, DFS 알고리즘 (with Python3)
그래프 BFS, DFS 알고리즘 (with Python3)
그래프 탐색 알고리즘에는 대표적으로 BFS 와 DFS 가 있다. 본 글에서는 아래 그래프를 가지고, BFS 와 DFS 의 탐색 알고리즘을 살펴본다. BFS 너비 우선 탐색을 BFS 라 부르고, Breadth Frist Search 의 약자이..
memostack.tistory.com
미로찾기 알고리즘
DFS, BFS 알고리즘을 이용해서 미로찾기 알고리즘을 구현할 수 있다.
문제 풀이의 핵심은 2가지이다.
- 미로 찾기 문제를 풀때는 미로를 모형화하여 그래프로 나타내는 것.
- 자료구조(
Stack또는Queue)에 노드(Node)와 비용(Cost) 을 같이 담는 것- 노드(
Node): 길(경로) - 비용(
Cost): 거리
- 노드(
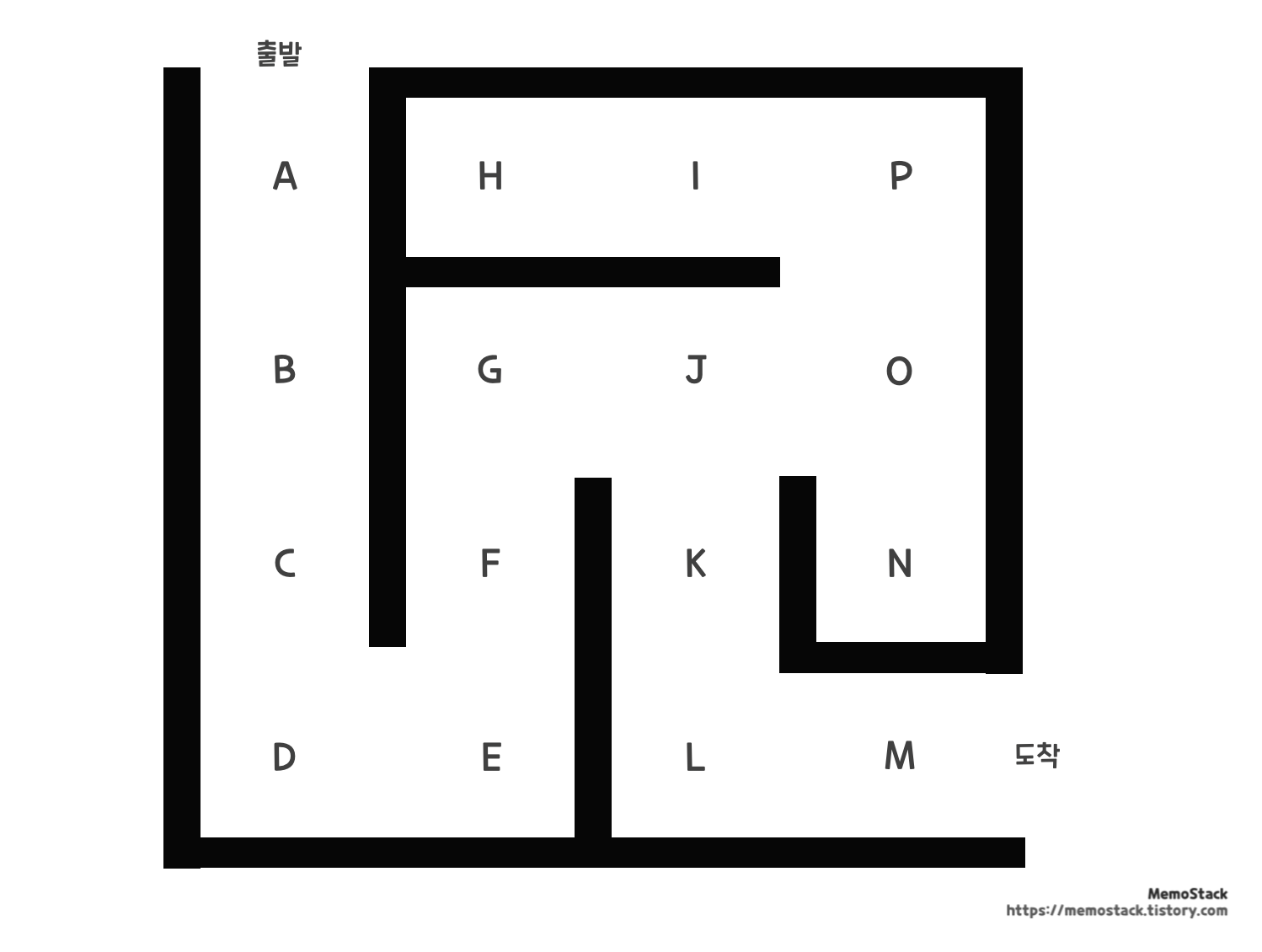
그래프 만들기
파이썬의 딕셔너리(Dictionary) 를 이용하여 그래프를 만든다.
# -*- coding: utf-8 -*-
import unittest
class Exam17(unittest.TestCase):
@classmethod
def setUp(cls):
cls.graph = {
"A": ["B"],
"B": ["A", "C"],
"C": ["B", "D"],
"D": ["C", "E"],
"E": ["D", "F"],
"F": ["E", "G"],
"G": ["F", "J"],
"H": ["I"],
"I": ["H", "P"],
"J": ["G", "K", "O"],
"K": ["J", "L"],
"L": ["K", "M"],
"M": ["L"],
"N": ["O"],
"O": ["J", "N", "P"],
"P": ["I", "O"]
}
# ...
DFS
깊이 우선 탐색으로 스택(Stack)을 이용하여 문제를 풀이한다.
# -*- coding: utf-8 -*-
import unittest
# ...
def dfs(graph, start, end):
"""DFS 를 이용하여 미로 찾기 알고리즘을 구현한다.
:param graph: 미로 그래프
:param start: 출발 지점(노드)
:param end: 도작 지점(노드)
:return: 최소 이동 거리
"""
stack = [(start, 0)] # idx 0: 노드, idx 1: 이동 거리
visit = {start, } # 방문한 노드 저장 공간
while stack:
node, distance = stack.pop()
new_distance = distance + 1
for near_node in graph[node]:
# 방문한 적 없는 노드인 경우
if near_node not in visit:
print("{} Node 방문".format(near_node))
# 도착 지점에 도착한 경우 총 이동거리를 반환
if near_node == end:
return new_distance
visit.add(near_node) # 방문
stack.append((near_node, new_distance)) # 이동 거리를 1 증가 시킨다.
return -1 # 도착 지점이 막힌 경우(없는 경우)
class Exam17(unittest.TestCase):
@classmethod
def setUp(cls):
cls.graph = {
"A": ["B"],
"B": ["A", "C"],
"C": ["B", "D"],
"D": ["C", "E"],
"E": ["D", "F"],
"F": ["E", "G"],
"G": ["F", "J"],
"H": ["I"],
"I": ["H", "P"],
"J": ["G", "K", "O"],
"K": ["J", "L"],
"L": ["K", "M"],
"M": ["L"],
"N": ["O"],
"O": ["J", "N", "P"],
"P": ["I", "O"]
}
# ...
def test_dfs(self):
self.assertEqual(10, dfs(self.graph, "A", "M"))
self.assertEqual(-1, bfs(self.graph, "A", "Z")) # Z 는 없는 노드
if __name__ == "__main__":
unittest.main()
BFS
너비 우선 탐색으로 큐(Queue)를 이용하여 문제를 풀이한다.
# -*- coding: utf-8 -*-
import unittest
def bfs(graph, start, end):
"""BFS 를 이용하여 미로 찾기 알고리즘을 구현한다.
:param graph: 미로 그래프
:param start: 출발 지점(노드)
:param end: 도작 지점(노드)
:return: 최소 이동 거리
"""
queue = [(start, 0)] # idx 0: 노드, idx 1: 이동 거리
visit = {start, } # 방문한 노드 저장 공간
while queue:
node, distance = queue.pop(0)
new_distance = distance + 1
for near_node in graph[node]:
# 방문한 적 없는 노드인 경우
if near_node not in visit:
print("{} Node 방문".format(near_node))
# 도착 지점에 도착한 경우 총 이동거리를 반환
if near_node == end:
return new_distance
visit.add(near_node) # 방문
queue.append((near_node, new_distance)) # 이동 거리를 1 증가 시킨다.
return -1 # 도착 지점이 막힌 경우(없는 경우)
# ...
class Exam17(unittest.TestCase):
@classmethod
def setUp(cls):
cls.graph = {
"A": ["B"],
"B": ["A", "C"],
"C": ["B", "D"],
"D": ["C", "E"],
"E": ["D", "F"],
"F": ["E", "G"],
"G": ["F", "J"],
"H": ["I"],
"I": ["H", "P"],
"J": ["G", "K", "O"],
"K": ["J", "L"],
"L": ["K", "M"],
"M": ["L"],
"N": ["O"],
"O": ["J", "N", "P"],
"P": ["I", "O"]
}
def test_bfs(self):
self.assertEqual(10, bfs(self.graph, "A", "M"))
self.assertEqual(-1, bfs(self.graph, "A", "Z")) # Z 는 없는 노드
# ...
if __name__ == "__main__":
unittest.main()
Reference
반응형
'Algorithm' 카테고리의 다른 글
| Programmers - 가장 큰 수 (Python3) (0) | 2020.04.02 |
|---|---|
| Programmers - K번째수 (Python3) (0) | 2020.04.02 |
| 탐색 알고리즘 BFS 응용하기 (친밀도 구하기) (0) | 2020.04.01 |
| 그래프 BFS, DFS 알고리즘 (with Python3) (0) | 2020.03.29 |
| 회문, 팰린드롬(Palindrome) 알고리즘 (with Python3) (0) | 2020.03.28 |
