블로그를 이전하였습니다. 2023년 11월부터 https://bluemiv.github.io/에서 블로그를 운영하려고 합니다. 앞으로 해당 블로그의 댓글은 읽지 못할 수 도 있으니 양해바랍니다.
반응형
본 글은Python3.7환경에서 진행합니다.unittest로 작성되어 있지만, 알고리즘을 확인하는데는 문제가 없습니다.
단순히 더하는 방법
결론부터 이야기 하자면 이 방법은 비효율적이다.
1 부터 10 까지 더하는 알고리즘을 작성하면 아래와 같이 생각할 수 있다.
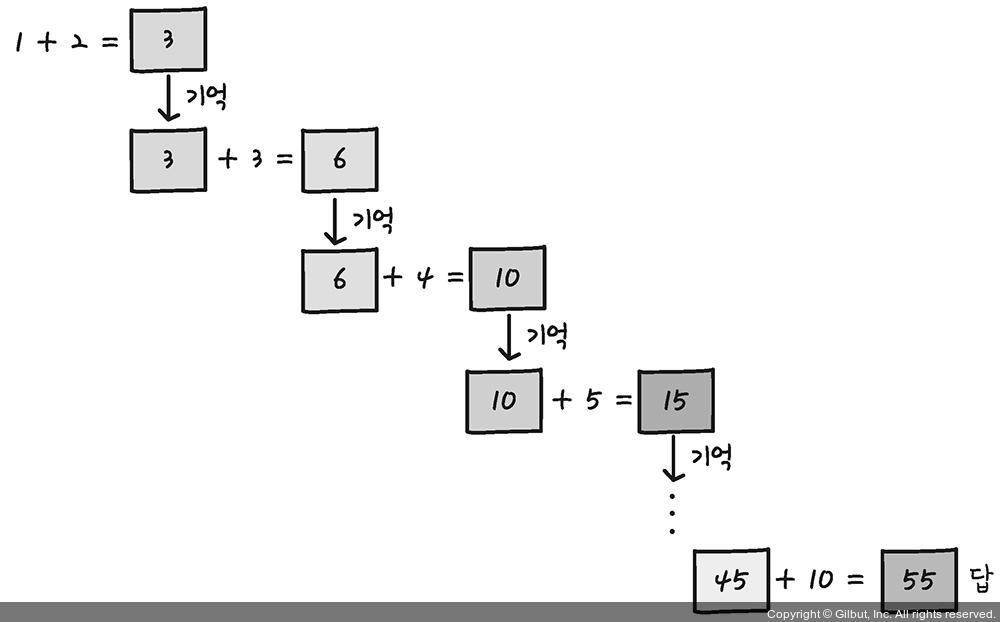
코드
test_sum 함수를 보자.
# -*- coding: utf-8 -*-
import unittest
class Exam01(unittest.TestCase):
def test_sum(self):
"""1 부터 n 까지 더하는 알고리즘"""
answer = 0 # 정답
for _ in range(1, 11):
answer += _ # 1 부터 10까지 더한다.
self.assertEqual(answer, 55)
if __name__ == "__main__":
unittest.main()
위 방식으로 문제를 풀어도 상관은 없지만, 숫자가 커질수록 비효율적이다.
가우스의 방법으로 문제 풀기
우리는 어렸을 적 가우스의 1 부터 100까지 더하기 일화를 한번쯤은 들어봤다. (몰라도 상관없음)
다른 친구들은 위 방법(단순히 더하는 방법)과 같이 문제를 풀었지만, 가우스는 달랐다.

여기서 가우스는 1 부터 n 더하기 문제의 공식을 발견했다.
n * (n + 1) / 2
위 공식으로 문제를 풀어보면... (사실 이해하면 되기 때문에 공식이라고 외울 필요없다)
코드
test_sum2 함수를 보자.
# -*- coding: utf-8 -*-
import unittest
class Exam01(unittest.TestCase):
...
def test_sum2(self):
"""가우스 방법으로 문제 풀기"""
n = 100
answer = n * (n + 1) // 2
self.assertEqual(answer, 5050)
if __name__ == "__main__":
unittest.main()
Python3에서는 나눗셈을 할때//를 사용하면 소숫점을 버리고 정수 부분만 반환한다.
반대로,/를 사용하면 소숫점까지 나오게 된다.
결론
가우스 방식을 사용하자.
- 숫자가 커질수록 단순히 더하는 방식은 연산량이 많아진다. 반면 가우스 방식으로 문제를 푸는 경우, 상대적으로 빠르게 답을 도출한다.
- n이 1억일때, 첫번째 방법은 4.842 초 걸리지만, 가우스 방식은 0.003초면 결과가 나온다.
- 시간 복잡도로 본다면, 첫번째 방법은
O(n)이고, 두번째 방법은O(1)이다. (시간복잡도: 2020/02/16 - [Algorithm] - 알고리즘의 시간 복잡도 - 빅오(O) 표기법)

Reference
- 모두의 알고리즘 with 파이썬 https://thebook.io/006935/
반응형
'Algorithm' 카테고리의 다른 글
| 집합을 이용한 중복 제거 알고리즘 (with Python3) (0) | 2020.03.16 |
|---|---|
| Java 스택(Stack)을 이용해서 순열 구하기 (0) | 2020.02.24 |
| Java 멱집합 구하기 (PowerSet) (0) | 2020.02.23 |
| 최댓값 찾기 알고리즘 (with Python3) (0) | 2020.02.19 |
| 알고리즘의 시간 복잡도 - 빅오(O) 표기법 (0) | 2020.02.16 |

